Systematische Programmentwicklung
Totale Korrektheit von While-Schleifen
Als Schlussregel für die While-Schleife hatten Sie bisher kennengelernt:
| P ∧ ¬B ⇒ R, {P ∧ B} S {P} |
| {P} while(B) S {R} |
Hierbei gilt die Nachbedingung R allerdings nur, wenn die Schleife verlassen wird, wenn sie also terminiert. Korrektheit unter dieser Voraussetzung wird als partielle Korrektheit bezeichnet.
Im Folgenden geht es darum, zusätzliche Bedingungen dafür zu finden, dass die Schleife auch terminiert.
Totale Korrektheit
Definition: Ein Programm S wird als partiell korrekt bezüglich einer Vorbedingung P und einer Nachbedingung Q bezeichnet, wenn es die Korrektheitsformel {P} S {Q} erfüllt, falls es terminiert. Als total korrekt wird es bezeichnet, wenn es die Korrektheitsformel {P} S {Q} erfüllt und terminiert.
Bedingungen für die Terminierung
Um zu beweisen, dass eine While-Schleife terminiert, suchen Sie nach einem ganzzahligen Ausdruck E, der
- beim Durchlauf durch den Schleifenkörper S stets vermindert wird,
- vor Ausführung des Schleifenkörpers S aber stets positiv ist.
Gibt es einen solchen ganzzahligen Ausdruck E, so kann die Schleife nicht unendlich oft durchlaufen werden, sondern muss irgendwann abbrechen.
Die Tatsache, dass der Ausdruck E vor Ausführung des Schleifenkörpers positiv ist, ist immer dann gegeben, wenn E > 0 aus P ∧ B folgt (Bild 1):
P ∧ B ⇒ E > 0.
Die Tatsache, dass der Ausdruck E beim Durchlauf durch den Schleifenkörper S vermindert wird, wenn dieser betreten wird, lässt sich so ausdrücken:
{P ∧ B} z=E; S {E < z}.
Hierbei ist z=E; eine zusätzliche Anweisung vor dem Schleifenkörper S und z eine neue Variable, die sonst nirgendwo vorkommt. Sie nimmt den Wert des ganzzahligen Ausdrucks E vor Ausführung von S auf. Nach Ausführung von S muss E kleiner als z sein, also in S vermindert worden sein.
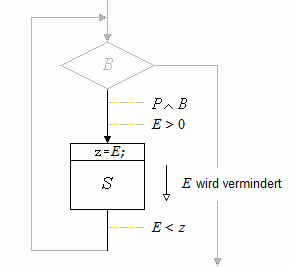
Bild 1: Ein ganzzahliger Ausdruck E wird im Schleifenkörper S vermindert
Schlussregel für die totale Korrektheit
Die Schlussregel für den Beweis der totalen Korrektheit der While-Schleife enthält die beiden Prämissen der Schlussregel für die partielle Korrektheit sowie zwei weitere Prämissen; sie lautet somit:
| P ∧ ¬B ⇒ R, {P ∧ B} S {P}, P ∧ B ⇒ E > 0, {P ∧ B} z=E; S {E < z} |
| {P} while (B) S {R} |
Um die totale Korrektheit einer While-Schleife zu beweisen, müssen Sie also vier Prämissen beweisen: 1.+2. die beiden Prämissen für die partielle Korrektheit, 3. die Tatsache, dass der ganzzahlige Ausdruck E vor Durchlaufen des Schleifenkörpers positiv ist und 4. die Tatsache, dass E beim Durchlaufen des Schleifenkörpers vermindert wird.
In den folgenden Beispielen werden diese vier Prämissen, bezeichnet mit While1, ..., While4, jeweils einzeln bewiesen.
Beispiel 1
Beispiel: Betrachten Sie die While-Schleife W mit Schleifenkörper S aus dem Programm zur Berechnung von n! :
{
i=i+1;
f=f*i;
}
Prämissen While1 und While2: Partielle Korrektheit
Die partielle Korrektheit hatten Sie bereits gezeigt.
Prämisse While3: Ganzzahliger Ausdruck E > 0
Für den Beweis der totalen Korrektheit benötigen Sie einen ganzzahligen Ausdruck E, der beim Eintritt in den Schleifenkörper positiv ist und im Schleifenkörper vermindert wird. Die ganzzahlige Variable i wird dort um 1 vermehrt, also wird der Ausdruck n-i vermindert.
Tatsächlich gilt mit
E: n-i,
dass
P ∧ B ⇒ E > 0
gilt, denn mit B: i < n ergibt sich sofort
P ∧ B ⇒ B ⇒ n > i ⇒ n-i > 0.
Prämisse While4: Ausdruck E wird im Schleifenkörper vermindert
Es ist zu zeigen:
{P ∧ B} z=E; S {E < z}.
Mit E: n-i führen Sie den Beweis wie folgt:
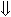 | { P ∧ B } | (9) |
| { true } | (8) | |
| { -1 < 0 } | (7) | |
| { n-i-1 < n-i } | (6) | |
| z=n-i; | ||
| { n-i-1 < z } | (5) | |
| { n-(i+1) < z } | (4) | |
| i=i+1; | ||
| { n-i < z } | (3) | |
| f=f*i; | ||
| { n-i < z } | (2) | |
| { E < z } | (1) |
Damit haben Sie insgesamt die totale Korrektheit der While-Schleife W gezeigt.
Die Schleifeninvariante P ist beim Beweis der Terminierung hier gar nicht eingegangen. Dies ist jedoch nicht immer so; im Allgemeinen können Sie die Terminierung nur im Zusammenhang mit einer geeigneten Bedingung P zeigen. Dies wird in dem nächsten Beispiel deutlich.
Beispiel 2: Schärfere Vorbedingung
Oft ist für den Beweis der totalen Korrektheit einer While-Schleife eine schärfere Vorbedingung P erforderlich als für den Beweis der partiellen Korrektheit.
Schärfere Vorbedingung für Terminierung
In folgendem Beispiel führen Sie eine bestimmte Vorbedingung P eigens für den Zweck ein, um die Terminierung der Schleife beweisen zu können.
Beispiel: Betrachten Sie folgende While-Schleife W mit Schleifenkörper S:
i=i-1;
Im Sinne der partiellen Korrektheit gilt {P} W {R} mit P: true und R: i = 0 sowie B: i ≠ 0 bzw: ¬B: i = 0.
Denn für die Prämisse While1 gilt hier
P ∧ ¬B ⇒ true ∧ i = 0 ⇒ i = 0 ⇒ R
Und der Beweis der Prämisse While2 lautet
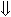 | { P ∧ B } | (5) |
| { true } | (4) | |
| z=i; | ||
| { true } | (3) | |
| i=i-1; | ||
| { true } | (2) | |
| { P } | (1) |
Für den Beweis der totalen Korrektheit benötigen Sie einen ganzzahligen Ausdruck E, der im Schleifenkörper vermindert wird und der vor dem Eintritt in den Schleifenkörper stets positiv ist. Weder aus P noch aus B lässt sich hier jedoch ein solcher Ausdruck ableiten.
Tatsächlich terminiert die Schleife auch nicht, wenn i zu Beginn negativ ist. Sie müssen also gewährleisten, dass i zu Beginn nicht negativ ist, indem Sie eine schärfere Vorbedingung P verwenden:
P: i ≥ 0
Mit dieser neuen Bedingung P: i ≥ 0 und der Nachbedingung R: i = 0 beweisen Sie zunächst die partielle Korrektheit.
Prämisse While1
Für die Prämisse While1 gilt hier
P ∧ ¬B ⇒ i ≥ 0 ∧ i = 0 ⇒ i = 0 ⇒ R
Prämisse While2
Der Beweis der Prämisse While2 lautet
| { P ∧ B } | (7) | |
| { i ≥ 0 ∧ i ≠ 0 } | (6) | |
| { i > 0 } | (5) | |
| { i ≥ 1 } | (4) | |
| { i-1 ≥ 0 } | (3) | |
| i=i-1; | ||
| { i ≥ 0 } | (2) | |
| { P } | (1) |
Prämisse While3: Ganzzahliger Ausdruck E > 0
Mit dem Ausdruck
E: i
gilt offenbar
P ∧ B ⇒ E > 0,
denn mit P: i ≥ 0 und B: i ≠ 0 sowie E: i ergibt sich
P ∧ B ⇒ i ≥ 0 ∧ i ≠ 0 ⇒ i > 0 ⇒ E > 0.
Prämisse While4: Ausdruck E wird im Schleifenkörper vermindert
Es ist zu zeigen:
{P ∧ B} z=E; S {E < z}.
Mit E: i lässt sich der Beweis wie folgt führen:
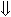 | { P ∧ B } | (7) |
| { true } | (6) | |
| { 0 < 1 } | (5) | |
| { i-1 < i } | (4) | |
| z=i; | ||
| { i-1 < z } | (3) | |
| i=i-1; | ||
| { i < z } | (2) | |
| { E < z } | (1) |
Sie haben nun alle vier Prämissen der Schlussregel für die totale Korrektheit der While-Schleife bewiesen. Damit haben Sie insgesamt die totale Korrektheit der While-Schleife W bezüglich der Vorbedingung P: i ≥ 0 und der Nachbedingung Q: i = 0 gezeigt.
Beispiel 3: Triviale While-Schleife
Die Aussagekraft der Schlussregel für die totale Korrektheit wird deutlich, wenn es gelingt, auch triviale While-Schleifen damit zu beweisen. Hierzu dient das folgende Beispiel.
Beispiel: Betrachten Sie folgende While-Schleife W mit leerem Schleifenkörper S:
Prämissen While1 und While2: Partielle Korrektheit
Offenbar gilt {true} W {true} im Sinne der partiellen Korrektheit mit P: true und R: true sowie B: false bzw. ¬B: true .
Denn für die Prämisse While1 gilt
P ∧ ¬B ⇒ true ∧ true ⇒ true ⇒ R
Und der Beweis der Prämisse While2 lautet
 | { P ∧ B } | (4) |
 | { true ∧ false } | (3) |
| { true } | (2) | |
| { P } | (1) |
Prämisse While3: Ganzzahliger Ausdruck E > 0
Für den Beweis der totalen Korrektheit benötigen Sie einen ganzzahligen Ausdruck E, der vor Eintritt in den Schleifenkörper positiv ist und im Schleifenkörper vermindert wird. Da der Schleifenkörper leer ist, kann eigentlich dort nichts vermindert werden. Versuchen Sie den Beweis trotzdem mit dem Ausdruck
E: 1
Offenbar gilt
P ∧ B ⇒ E > 0.
Prämisse While4: Ausdruck E wird im Schleifenkörper vermindert
Ferner ist zu zeigen:
{P ∧ B} z=E; S {E < z}.
Mit E: 1 lässt sich der Beweis wie folgt führen:
 | { P ∧ B } | (6) |
| { B } | (5) | |
| { false } | (4) | |
| { 1 < 1 } | (3) | |
| z=1; | ||
| { 1 < z } | (2) | |
| { E < z } | (1) |
Damit haben Sie insgesamt die totale Korrektheit dieser trivialen While-Schleife W gezeigt.
H.W. Lang mail@hwlang.de Impressum Datenschutz
Diese Webseiten sind größtenteils während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden